Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang cân, đáy lớn \(AD = 2a\), \(AB = BC = CD = a.\) Cạnh bên \(SA = 2a\) và vuông góc với đáy. Gọi \(R\) là bán kính mặt cầu ngoại tiếp khối chóp \(S.ABCD.\) Tỉ số \(\dfrac{R}{a}\) nhận giá trị nào sau đây ?
- A \(a\sqrt 2 .\)
- B \(2.\)
- C \(1.\)
- D \(\sqrt 2 .\)
Lời giải chi tiết:
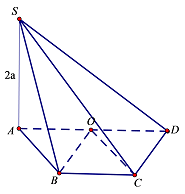
+ Gọi \(O\) là trung điểm \(AD \Rightarrow OA = OB = OC = OD = a\).
\(\begin{array}{l} \Rightarrow {{\rm{R}}_{day}} = a\\ \Rightarrow {R_{mcnt}} = \sqrt {{a^2} + \dfrac{{{{\left( {2a} \right)}^2}}}{4}} = a\sqrt 2 \end{array}\)
Chọn D.
Câu hỏi trước
