Lời giải chi tiết:

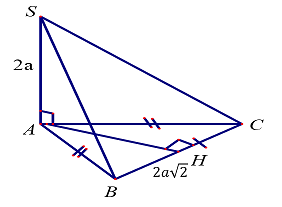
+ Gọi \(H\) là trung điểm \(BC \Rightarrow AH \bot BC\).

+ Xét \(\Delta AHB\) vuông tại \(H\) có: \(\widehat {HAB} + \widehat {ABC} = {90^0}\).

Mà \(\Delta ABC\)cân tại \(A \Rightarrow \widehat {ABC} = \widehat {ACB}\)

\( \Rightarrow \widehat {HAB} + \widehat {ACB} = {90^0}\)\( \Rightarrow \)2 góc phụ nhau.

\(\begin{array}{l} \Rightarrow \cos \widehat {ACB} = \sin \widehat {HAB} = \dfrac{1}{3}\\ \Rightarrow \widehat {HAB} \approx 19,{47^0} \Rightarrow \widehat {BAC} \approx 38,{94^0} \Rightarrow \sin \widehat {BAC} = \dfrac{{4\sqrt 2 }}{9}\end{array}\)

+) Xét \(\Delta ABC\) có: \(\dfrac{{BC}}{{\sin \widehat {BAC}}} = 2{r_{\Delta ABC}} \Rightarrow {r_{\Delta ABC}} = \dfrac{{BC}}{{2\sin \widehat {BAC}}} = \dfrac{{2a\sqrt 2 }}{{2\dfrac{{4\sqrt 2 }}{9}}} = \dfrac{{9a}}{4}\)

Bán kính mặt cầu ngoại tiếp chóp \(S.ABC\) là:

\(\begin{array}{l}R = \sqrt {{{\left( {\dfrac{h}{2}} \right)}^2} + {r^2}}  = \sqrt {{{\left( {\dfrac{{SA}}{2}} \right)}^2} + {{\left( {\dfrac{{9a}}{4}} \right)}^2}}  = \sqrt {\dfrac{{4{a^2}}}{4} + {{\left( {\dfrac{{9a}}{4}} \right)}^2}}  = \dfrac{{a\sqrt {97} }}{4}\\{S_{mc}} = 4\pi {R^2} = 4\pi .{\left( {\dfrac{{a\sqrt {97} }}{4}} \right)^2} = \dfrac{{97\pi {a^2}}}{4}\end{array}\)        

Chọn C