Lời giải chi tiết:

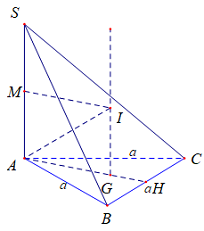
Dựng như hình vẽ ta có \(I\) là tâm mặt cầu ngoại tiếp và có \(R = IA\).

+ \(AG = \dfrac{2}{3}AH = \dfrac{2}{3}.\dfrac{{6\sqrt 3 }}{2} = \dfrac{{6\sqrt 3 }}{3} = 2\sqrt 3 \)

+ \(IG = \dfrac{1}{2}SA = \dfrac{1}{2}.4\sqrt 6  = 2\sqrt 6 \)

+Xét \(\Delta IAG\)vuông tại \(G\) có: 

\(I{A^2} = I{G^2} + A{G^2} = {\left( {2\sqrt 3 } \right)^2} + {\left( {2\sqrt 6 } \right)^2} = 36\)

\( \Rightarrow IA = 6 \Rightarrow {S_{mcnt}} = 4\pi {R^2} = 4\pi {6^2}\, = 144\pi .\)

Chọn D