Lời giải chi tiết:

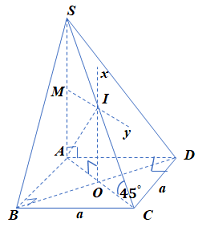
B1: Dựng \(Ox \bot day\,\,\,\left( {Ox\parallel SA} \right)\).

B2: Dựng tia trung trực \(My\parallel AC\) (\(M\) là trung điểm \(SA\)).

\( \Rightarrow Ox \cap My = I\)\( \Rightarrow I\) là tâm mặt cầu ngoại tiếp với \(R = IA\).

+ Gọi \(AC \cap BD = \left\{ O \right\}\).

+ Có \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\)cùng vuông góc với \(\left( {ABCD} \right)\).

\( \Rightarrow SA \bot \left( {ABCD} \right)\).

\( \Rightarrow \)Góc giữa \(SC\)và \(\left( {ABCD} \right)\) là \(\widehat {SCA} = {45^0}\).

\(ABCD\)là hình vuông cạnh \(a \Rightarrow AC = a\sqrt 2  \Rightarrow AO = \dfrac{{a\sqrt 2 }}{2}\).

+ Xét \(\Delta SAC\) vuông tại \(A\) có \(\widehat {SCA} = {45^0} \Rightarrow \Delta SAC\)vuông cân \( \Rightarrow SA = AC = a\sqrt 2 .\)  

Có: \(OI = \dfrac{1}{2}SA = \dfrac{{a\sqrt 2 }}{2}\)

Xét \(\Delta AIO\)vuông tại \(O\) có: \(A{I^2} = A{O^2} + O{I^2} = \dfrac{{{a^2}}}{2} + \dfrac{{{a^2}}}{2} = {a^2} \Rightarrow AI = a \Rightarrow R = a.\)

Chọn A