Câu hỏi
Cho hình trụ có hai đáy là hình tròn \(\left( O \right)\) và \(\left( {O'} \right)\). Trên hai đường tròn lấy hai điểm \(A,\,\,B\) sao cho góc giữa \(AB\) và mặt phẳng chứa đường tròn đáy bằng \({45^0}\) và khoảng cách đến trục \(OO'\) bằng \(\dfrac{{a\sqrt 2 }}{2}\). Biết bán kính đáy bằng \(a\), tính thể tích của khối trụ theo \(a\).
- A \(V = \dfrac{{\pi {a^3}\sqrt 2 }}{6}.\)
- B \(V = \pi {a^3}\sqrt 2 .\)
- C \(V = \dfrac{{\pi {a^3}\sqrt 2 }}{2}.\)
- D \(V = \dfrac{{\pi {a^3}\sqrt 2 }}{3}.\)
Lời giải chi tiết:
Đặt \(OO' = h\).
+ Kẻ \(AC\parallel OO' \Rightarrow AC \bot \) (đáy)
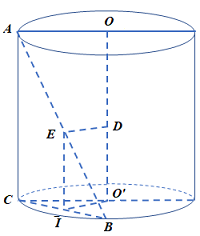
\( \Rightarrow \widehat {(AB,day)} = \widehat {ABC} = {45^0}\)
\( + \) Gọi \(I\) là trung điểm \(BC\).
\( + \) Ta có: \(d\left( {AB;OO'} \right) = d\left( {\left( {ABC} \right),OO'} \right) = d\left( {O',\left( {ABC} \right)} \right) = O'I\)
\( \Rightarrow O'I = \dfrac{{a\sqrt 2 }}{2}\).
\( + \) Vì \(\Delta ABC\) vuông cân tại \(C \Rightarrow BC = AC = h\)
\( + \) Lại có: \(CO{'^2} = C{I^2} + IO{'^2}\)
\( \Leftrightarrow {a^2} = {\left( {\dfrac{{BC}}{2}} \right)^2} + {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2} \Rightarrow BC = a\sqrt 2 = h\)
\( + \,\,V = \pi {R^2}h = \pi {a^2}.a\sqrt 2 = \pi {a^3}\sqrt 2 \).
Chọn B







