Câu hỏi
Cho một hình trụ có hai đáy là hình tròn \(\left( {O;R} \right)\) và \(\left( {O';R} \right)\) với \(OO' = R\sqrt 3 \) và một hình nón có đỉnh \(O'\) và đáy là hình tròn \(\left( {O;R} \right)\). Kí hiệu \({S_1},\,\,{S_2}\) lần lượt là diện tích xung quanh của hình trụ và hình nón. Tính \(k = \dfrac{{{S_1}}}{{{S_2}}}\)?
- A \(k = \dfrac{1}{3}\)
- B \(k = \sqrt 2 \)
- C \(k = \sqrt 3 \)
- D \(k = \dfrac{1}{2}\)
Lời giải chi tiết:
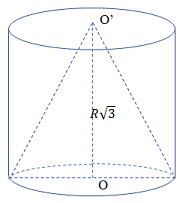
\(\begin{array}{l} + \,\,{S_1} = 2\pi Rh = 2\pi R.R\sqrt 3 = 2\pi {R^2}\sqrt 3 \\ + \,\,{S_2} = \pi Rl = \pi R\sqrt {{{\left( {R\sqrt 3 } \right)}^2} + {R^2}} = \pi 2.{R^2}\\ \Rightarrow K = \dfrac{{{S_1}}}{{{S_2}}} = \sqrt 3 .\end{array}\)
Chọn C
Câu hỏi trước
