Câu hỏi
Cho hình nón tròn xoay có chiều cao \(h = 20\,\left( {{\rm{cm}}} \right)\), bán kính đáy \(r = 25\,\left( {{\rm{cm}}} \right)\). Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là \(12\,\left( {{\rm{cm}}} \right)\). Tính diện tích của thiết diện đó.
- A \(S = 500\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
- B \(S = 400\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
- C \(S = 300\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
- D \(S = 406\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Lời giải chi tiết:
\( + \)Khoảng cách từ tâm đáy đến thiết diện: \(d\left( {O;\left( {SAB} \right)} \right)\)
+ Kẻ \(OH \bot AB\) (\(H\) trung điểm \(AB\))
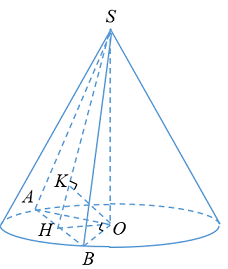
\(OK \bot SH\)
\( \Rightarrow d\left( {O,SAB} \right) = OK = 12\)
\( + \)\(\Delta SHO\) vuông tại \(O\) có đường cao \(OK\).
\(\begin{array}{l} \Rightarrow \dfrac{1}{{O{K^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{H^2}}} \Leftrightarrow \dfrac{1}{{{{12}^2}}} = \dfrac{1}{{{{20}^2}}} + \dfrac{1}{{O{H^2}}}\\ \Leftrightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{225}} \Leftrightarrow OH = 15\left( {cm} \right)\end{array}\)
\( + \)\(\Delta OHB\)vuông tại \(H\) có:
\(O{H^2} + B{H^2} = O{B^2} \Leftrightarrow B{H^2} = {25^2} - {15^2} \Leftrightarrow BH = 20\left( {cm} \right)\).
\( \Rightarrow AB = 2BH = 40\,\,\left( {cm} \right)\)
\( + \)\(S{H^2} = S{O^2} + O{H^2} = {20^2} + {15^2} = {25^2}\) \( \Leftrightarrow SH = 25\left( {cm} \right)\)
\( + \)\({S_{\Delta SAB}} = \dfrac{1}{2}.SH.AB = \dfrac{1}{2}.25.40 = 500\left( {c{m^2}} \right)\).
Chọn A







