Câu hỏi
Cho hình nón đỉnh \(S\), góc ở đỉnh bằng \({120^0}\), đáy là hình tròn \(\left( {O;3R} \right)\). Cắt hình nón bởi mặt phẳng qua \(S\) và tạo với đáy góc \({60^0}\). Diện tích thiết diện là:
- A
\(2\sqrt 2 {R^2}\)
- B \(4\sqrt 2 {R^2}\)
- C \(6\sqrt 2 {R^2}\)
- D \(8\sqrt 2 {R^2}\)
Lời giải chi tiết:
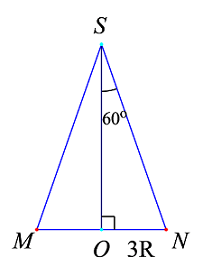
\( + \) Thiết diện qua trục là tam giác \(SMN \Rightarrow \widehat {MSN} = {120^0} \Rightarrow \widehat {OSN} = {60^0}\).
Ta có: \(SO = \dfrac{{ON}}{{\tan {{60}^0}}} = \dfrac{{3R}}{{\sqrt 3 }} = R\sqrt 3 \)
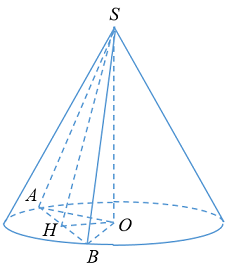
\( + \)\(\left( {SAB} \right)\) tạo với đáy góc \({60^0} \Rightarrow \widehat {SHO} = {60^0}\)
\( + \)\(OH = \dfrac{{SO}}{{\tan {{60}^0}}} = \dfrac{{R\sqrt 3 }}{{\sqrt 3 }} = R.\)
+ Ta có:\(S{O^2} + O{H^2} = S{H^2} \Leftrightarrow {\left( {R\sqrt 3 } \right)^2} + {R^2} = S{H^2} \Leftrightarrow SH = 2R\)
\( + \)\(O{H^2} + H{B^2} = O{B^2} \Leftrightarrow H{B^2} = {\left( {3R} \right)^2} - {R^2} \Leftrightarrow HB = 2R\sqrt 2 \)
\( \Rightarrow AB = 2HB = 4R\sqrt 2 \)
\( + \)\({S_{\Delta SAB}} = \dfrac{1}{2}.SH.AB = \dfrac{1}{2}.2R.4R\sqrt 2 = 4\sqrt 2 .{R^2}\).
Chọn B







