Câu hỏi
Cắt mặt xung quanh của một hình nón dọc theo một đường sinh rồi trải ra trên mặt phẳng ta được một nửa hình tròn bán kính \(R\). Tính thể tích khối nón được tạo nên từ hình nón đó?
- A \(\dfrac{{{R^3}\sqrt 3 }}{8}\)
- B \(\dfrac{{{R^3}\sqrt 3 }}{{24}}\)
- C \(\dfrac{{{R^3}}}{{24}}\)
- D \(\dfrac{{{R^3}\sqrt 3 }}{{12}}\)
Phương pháp giải:
Lời giải chi tiết:
Ta có \({R_{tron}} = {l_{non}}\)
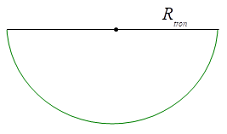
Chu vi nửa hình tròn = Chu vi đáy hình nón
\( \Rightarrow \pi {R_{tron}} = 2\pi {R_{non}} \Leftrightarrow {R_{non}} = \dfrac{{{R_{tron}}}}{2}\)
\(\begin{array}{l}{h_{non}} = \sqrt {{l_{non}}^2 - {r_{non}}^2} \\\,\,\,\,\,\,\,\,\, = \sqrt {{R_{tron}}^2 - {{\left( {\dfrac{{{R_{tron}}}}{2}} \right)}^2}} = \dfrac{{\sqrt 3 {R_{tron}}}}{2}\\{V_{non}} = \dfrac{1}{3}\pi .{r^2}.h = \dfrac{1}{3}\pi .{\left( {\dfrac{{{R_{tron}}}}{2}} \right)^2}.\dfrac{{\sqrt 3 {R_{tron}}}}{2} = \dfrac{{\pi {R^3}_{tron}\sqrt 3 }}{{24}}\end{array}\)
Chọn B
Câu hỏi trước
