Câu hỏi
Cắt hình nón đỉnh \(S\) bởi mặt phẳng đi qua trục, ta được một tam giác vuông cân có cạnh huyền bằng \(2a\). Thể tích của khối nón là:
- A \(\dfrac{{\pi {a^3}\sqrt 2 }}{{12}}\)
- B \(\dfrac{{\pi {a^3}}}{3}\)
- C \(\dfrac{{\pi {a^3}\sqrt 2 }}{2}\)
- D \(\pi {a^3}\)
Lời giải chi tiết:
+ Thiết diện qua trục là\(\Delta ABC\)vuông cân tại \(A\) có \(BC = 2a\)
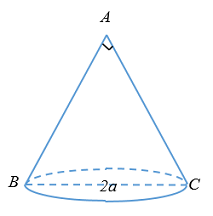
\( \Rightarrow R = \dfrac{1}{2}BC = \dfrac{1}{2}.2a = a.\)
+ Gọi \(O\) là trung điểm \(BC\).
+ \(h = AO = \dfrac{1}{2}BC = a\) (tam giác vuông có đường trung tuyến bằng nửa cạnh huyền).
\( \Rightarrow \) \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .{a^2}.a = \dfrac{{\pi {a^3}}}{3}\).
Chọn B
Câu hỏi trước
