Câu hỏi
Cắt khối nón bởi mặt phẳng qua trục, thiết diện tạo thành là một tam giác đều \(ABC\) cạnh bằng \(a\) và \(B,\,\,C\) thuộc đường tròn đáy. Thể tích của khối nón là:
- A \(\dfrac{{2\sqrt 3 \pi {a^3}}}{9}\)
- B \(\dfrac{{3\pi {a^3}}}{8}\)
- C \(\dfrac{{\sqrt 3 \pi {a^3}}}{{24}}\)
- D \(\sqrt 3 \pi {a^3}\)
Lời giải chi tiết:
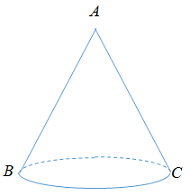
Thiết diện qua trục là \(\Delta ABC\)đều cạnh \(a\):
\( \Rightarrow \)\(\left\{ \begin{array}{l}l = a\\h = \dfrac{{a\sqrt 3 }}{2}\\R = \dfrac{a}{2}\end{array} \right. \Rightarrow {V_{non}} = \dfrac{1}{3}\pi {R^2}.h = \dfrac{{\pi {a^3}\sqrt 3 }}{{24}}\)
Chọn C
Câu hỏi trước
