Câu hỏi
Cho hình chóp \(S.ABC\) có \(SA = SB = SC = 4,\,\,AB = BC = CA = 3\). Tính thể tích khối nón giới hạn bởi hình nón có đỉnh là \(S\) và đáy là đường tròn ngoại tiếp \(\Delta ABC\).
- A \(2\sqrt 2 \pi \)
- B \(3\pi \)
- C \(\sqrt {13} \pi \)
- D \(4\pi \)
Lời giải chi tiết:
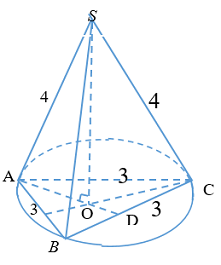
+ Gọi \(D\) là trung điểm của \(BC\).
+ Gọi \(O\) là tâm đường tròn ngoại tiếp \(\Delta ABC \Rightarrow SO \bot \left( {ABC} \right)\).
+ Hình nón ngoại tiếp chóp \(S.ABCD\) có\(\left\{ \begin{array}{l}R = OA\\h = SO\end{array} \right.\)
+ \(\Delta ABC\) đều cạnh cạnh 3 \( \Rightarrow \)\(AD = \dfrac{{3\sqrt 3 }}{2} \Rightarrow AO = \dfrac{2}{3}.AD \Rightarrow AO = \sqrt 3 \)
+ Xét\(\Delta SAO\) vuông tại \(O\) có: \(S{A^2} = S{O^2} + A{O^2}\)
\( \Rightarrow S{O^2} = {4^2} - {\left( {\sqrt 3 } \right)^2} = 13 \Rightarrow SO = \sqrt {13} \)
+ \({V_{non}} = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}.3\pi .\sqrt {13} = \sqrt {13} \pi .\)
Chọn C
Câu hỏi trước
