Câu hỏi
Một hình nón có đường cao \(h = a\sqrt 3 \) và bán kính mặt đáy \(R = a\) được cắt ra theo một đường sinh rồi trải ra trên mặt phẳng ta được 1 hình quạt . Tính góc ở tâm \(\alpha \) của hình quạt đó?
- A \(\alpha = \dfrac{\pi }{6}\)
- B \(\alpha = \dfrac{\pi }{3}\)
- C \(\alpha = \pi \)
- D \(\alpha = \dfrac{{2\pi }}{3}\)
Lời giải chi tiết:
+ Khi trải hình nón ta thấy \({S_{xq}}\) = Shình quạt
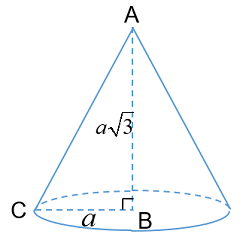
+ Xét \(\Delta ABC\) vuông tại \(B\) có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} = 3{a^2} + {a^2} = 4{a^2}\\ \Rightarrow AC = 2a \Rightarrow l = 2a\end{array}\)
+ \({S_{xq}} = \pi Rl = \pi .a.2a = 2\pi {a^2}\)
+ Shình quạt \( = \dfrac{{\pi {l^2}\alpha }}{{360}}\).
Mà \({S_{xq}}\) = Shình quạt
\( \Rightarrow 2\pi {a^2} = \dfrac{{\pi {l^2}\alpha }}{{360}} \Rightarrow \alpha = \dfrac{{2\pi {a^2}.360}}{{\pi {l^2}}} = {180^0}\)
(\(\alpha \)là góc ở đỉnh hình quạt)
\( \Rightarrow \alpha = {180^0} \Rightarrow \alpha = \pi \)
Chọn C
Câu hỏi trước
