Câu hỏi
Hình nón tròn xoay ngoại tiếp tứ diện đều cạnh bằng \(a\), có diện tích xung quanh là:
- A \({S_{xq}} = \dfrac{{\pi {a^2}\sqrt 2 }}{3}\).
- B \({S_{xq}} = \dfrac{{\pi {a^2}}}{3}\).
- C \({S_{xq}} = \dfrac{{\pi {a^2}\sqrt 3 }}{6}\).
- D \({S_{xq}} = \dfrac{{\pi {a^2}\sqrt 3 }}{3}\)
Lời giải chi tiết:
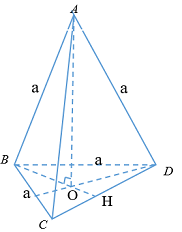
+ Gọi \(H\) là trung điểm \(CD\).
+ \(O\) là trọng tâm \(\Delta BCD\)\( \Rightarrow AO \bot \left( {BCD} \right)\).
+ Hình nón ngoại tiếp tứ diện đều có \(\left\{ \begin{array}{l}R = OB\\l = AB = a\end{array} \right.\)
+\(\Delta BCD\) đều cạnh \(a \Rightarrow BH = \dfrac{{a\sqrt 3 }}{2}\).
Mà \(BO = \dfrac{2}{3}BH = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3} \Rightarrow R = \dfrac{{a\sqrt 3 }}{3}\)
+ \({S_{xq}} = \pi Rl = \pi .BO.BA = \pi .\dfrac{{a\sqrt 3 }}{3}.a = \dfrac{{\pi {a^2}\sqrt 3 }}{3}\).
Chọn D
Câu hỏi trước
