Câu hỏi
Trong không gian cho tam giác \(ABC\) có \(AB = AC = 4\) và \(BC = 6\). Gọi \(M\) là trung điểm của cạnh \(BC\). Quay tam giác đó quanh trục \(AM\) ta được một hình nón. Tính diện tích toàn phần \({S_{tp}}\) của hình nón đó?
- A \({S_{tp}} = 21\pi \)
- B \({S_{tp}} = 29\pi \)
- C \({S_{tp}} = 24\pi \)
- D \({S_{tp}} = 7\pi \)
Lời giải chi tiết:
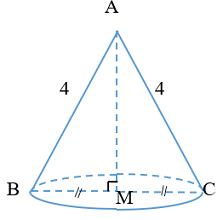
+ Có: \(AB = AC \Rightarrow \Delta ABC\) cân tại \(A\). Mà \(M\) là trung điểm \(BC \Rightarrow AM \bot BC\).
+ \(R = MC = \dfrac{1}{2}BC = 3\).
+ \(l = AC = 4\)
+ \({S_{xq}}\, = \,\pi Rl = \pi .MC.AC = \pi .3.4 = 12\pi \)
+ \({S_d} = \pi {R^2} = \pi {.3^2} = 9\pi \)
Vậy \({S_{tp}} = {S_{xq}} + {S_d} = 12\pi + 9\pi = 21\pi .\)
Chọn A
Câu hỏi trước
