Câu hỏi
Một hình nón có góc ở đỉnh bằng \(2\alpha \,\,\left( {{0^0} < 2\alpha < {{180}^0}} \right)\) và khoảng cách từ tâm của đường tròn đáy đến mỗi đường sinh bằng \(d\).Tính theo \(d\) và \(\alpha \) chiều cao \(h\) của hình nón?
- A \(h = \dfrac{d}{{\sin \alpha }}\)
- B \(h = \dfrac{d}{{\cos \alpha }}\)
- C \(h = \dfrac{d}{{\tan \alpha }}\)
- D \(h = \dfrac{d}{{\cot \alpha }}\)
Lời giải chi tiết:
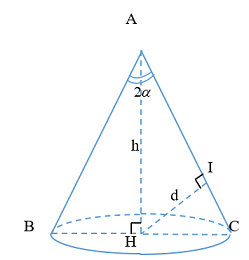
+ Ta có: \(\widehat {BAC} = 2\alpha \Rightarrow \widehat {HAC} = \alpha \)
+ Xét \(\Delta AHI\) vuông tại \(I\) có: \(\sin \widehat {HAI} = \dfrac{{HI}}{{AH}}\)
\( \Leftrightarrow \sin \alpha \, = \dfrac{d}{h}\, \Leftrightarrow h = \dfrac{d}{{\sin \alpha }}\)
Chọn A
Câu hỏi trước
