Câu hỏi
Một hình nón được sinh ra do tam giác đều cạnh \(2a\) quay quanh đường cao của nó.Khoảng cách từ tâm của đáy đến đường sinh của nón bằng:
- A \(\dfrac{{a\sqrt 3 }}{3}\)
- B \(\dfrac{{a\sqrt 3 }}{2}\)
- C \(a\sqrt 2 \)
- D \(a\sqrt 3 \)
Lời giải chi tiết:
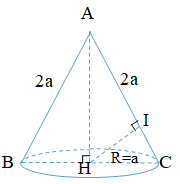
+ Gọi chân đường cao hạ từ \(H\) xuống \(AC\) là \(I\).
\( \Rightarrow HI\) là khoảng cách từ tâm của đáy hình nónđến đường sinh.
+ Vì \(\Delta ABC\) đều cạnh \(2a\)\( \Rightarrow AH = 2a\dfrac{{\sqrt 3 }}{2} = a\sqrt 3 \)
+ Xét \(\Delta AHC\) vuông tại \(H\) có:
\(\dfrac{1}{{H{I^2}}} = \dfrac{1}{{A{H^2}}} + \dfrac{1}{{H{C^2}}}\)
\( \Leftrightarrow \dfrac{1}{{H{I^2}}} = \dfrac{1}{{3{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{4}{{3{a^2}}} \Rightarrow HI = \dfrac{{3{a^2}}}{4} \Rightarrow HI = \dfrac{{a\sqrt 3 }}{2}\)
Chọn B
Câu hỏi trước
