Phương pháp giải:

a) Làm theo các bước khảo sát và vẽ đồ thị hàm số

b) Dựa vào đồ thị tìm giá trị lớn nhất, giá trị nhỏ nhất trên đoạn.

Lời giải chi tiết:

Cho hàm số \(y = f(x) = {x^2} - 4x\).

a) Lập bảng biến thiên và vẽ đồ thị hàm số \(y = f\left( x \right).\)

* Tập xác định: \(D = \mathbb{R}\)

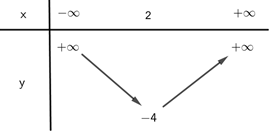
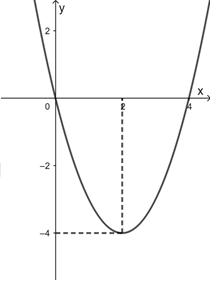
* Đỉnh: \(I\left( {2; - 4} \right),\,\,\,a = 1 > 0,\) trục đối xứng của đồ thị hàm số là: \(x = 2\)

* Giao điểm của đồ thị với trục tung là: \(O\left( {0;\,\,0} \right).\)

Ta có:   \(y = 0 \Rightarrow {x^2} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 4\end{array} \right..\)

\( \Rightarrow \) Giao điểm của đồ thị với trục hoành là: \(\left( {0;\,\,0} \right),\,\,\left( {4;\,\,0} \right).\)

* Bảng biến thiên

* Đồ thị:

b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f(x)\)trên đoạn \(\left[ {0;4} \right]\)

Dựa vào đồ thị hàm số trên đoạn \(\left[ {0;4} \right]\) ta có:

\(\mathop {Max}\limits_{\left[ {0;\,\,4} \right]} f\left( x \right) = 0\) khi \(x = 0\) hoặc \(x = 4.\)

\(\mathop {Min}\limits_{\left[ {0;\,\,4} \right]} f\left( x \right) =  - 4\) khi \(x = 2\).

Chọn A.