Câu hỏi
Gọi M, N, I là các điểm trên một lò xo nhẹ, được treo thẳng đứng ở điểm O cố định. Khi lò xo có chiều dài tự nhiên thì OM = MN = NI = 10 cm. Gắn vật nhỏ vào đầu dưới I của lò xo và kích thích để vật dao động điều hòa theo phương thẳng đứng. Trong quá trình dao động, tỉ số độ lớn lực kéo lớn nhất và độ lớn lực kéo nhỏ nhất tác dụng lên O bằng 3, lò xo giãn đều, khoảng cách lớn nhất giữa hai điểm M và N là 12 cm. Lấy \({\pi ^2} = 10\). Vật dao động với tần số là
- A 2,9 Hz
- B 2,5 Hz
- C 3,5 Hz
- D 1,7 Hz
Phương pháp giải:
Tần số dao động: \(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} = \frac{1}{{2\pi }}\sqrt {\frac{g}{{\Delta l}}} \)
Độ lớn lực đàn hồi tác dụng lên điểm treo: \({F_{dh}} = k.\Delta l\)
Lời giải chi tiết:
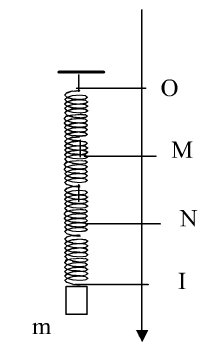
Trong quá trình dao động, lò xo luôn giãn \( \to A < \Delta l\)
Chiều dài tự nhiên của lò xo: \({l_0} = 3.10 = 30\,\,\left( {cm} \right)\)
Tỉ số độ lớn lực kéo lớn nhất và độ lớn lực kéo nhỏ nhất tác dụng lên điểm treo:
\(\frac{{{F_{dh\max }}}}{{{F_{dh\min }}}} = \frac{{k.\left( {\Delta {l_0} + A} \right)}}{{k.\left( {\Delta {l_0} - A} \right)}} = 3 \Rightarrow \frac{{\Delta {l_0} + A}}{{\Delta {l_0} - A}} = 3 \Rightarrow \Delta {l_0} = 2A\)
Chiều dài lớn nhất của lò xo:
\({l_{\max }} = {l_0} + \Delta l + A \Rightarrow 30 + 3A = 3.12 \Rightarrow A = 2\,\,\left( {cm} \right) \Rightarrow \Delta {l_0} = 2A = 4\,\,\left( {cm} \right)\)
Tần số dao động: \(f = \frac{1}{{2\pi }}\sqrt {\frac{g}{{\Delta l}}} = \frac{1}{{2\pi }}\sqrt {\frac{{10}}{{0,04}}} = 2,5\,\,\left( {Hz} \right)\)
Chọn B.







