Phương pháp giải:

Sử dụng vòng tròn lượng giác và công thức: \(\Delta t = \frac{{\Delta \varphi }}{\omega }\)

Áp dụng công thức độc lập với thời gian: \({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\)

Công thức độ lớn lực đàn hồi: \({F_{dh}} = k.\Delta l\)

Lời giải chi tiết:

Trong khoảng thời gian lò xo nén, vật quay được góc:

 \(\Delta \varphi  = \omega .\Delta t = \frac{{2\pi }}{T}.\frac{T}{6} = \frac{\pi }{3}\,\,\left( {rad} \right)\)

Biểu diễn trên VTLG, ta có:

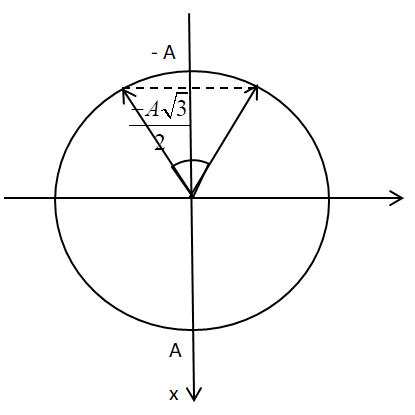
Từ VTLG, ta thấy tại thời điểm lò xo không biến dạng, vật có li độ \(x = \frac{{ - A\sqrt 3 }}{2}\) và có tốc độ \(10\pi \sqrt 3 \,\,cm/s\)

Áp dụng công thức độc lập với thời gian, ta có:

 \({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow {\left( {\frac{{ - A\sqrt 3 }}{2}} \right)^2} + \frac{{{{\left( {0,1\pi \sqrt 3 } \right)}^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow A.\omega  = 0,2\pi \sqrt 3 \,\,\left( 1 \right)\)

Ở vị trí cân bằng, lò xo giãn một đoạn:

 \(\Delta l =  - x \Rightarrow \frac{{mg}}{k} = \frac{{A\sqrt 3 }}{2} \Rightarrow \frac{g}{{{\omega ^2}}} = \frac{{A\sqrt 3 }}{2} \Rightarrow A.{\omega ^2} = \frac{{2g}}{{\sqrt 3 }} = \frac{{20}}{{\sqrt 3 }}\,\,\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow \left\{ \begin{gathered}A = 0,06\sqrt 3 \,\,\left( m \right) \hfill \\\omega = \frac{{10\pi }}{3}\,\,\left( {rad/s} \right) \hfill \\ \end{gathered} \right.\)

Ở vị trí lò xo có chiều dài ngắn nhất, lực đàn hồi tác dụng lên vật là:

 \({F_{dh}} = k.\left( {A - \frac{{A\sqrt 3 }}{2}} \right) = k.A.\left( {1 - \frac{{\sqrt 3 }}{2}} \right) = 100.0,06\sqrt 3 .\left( {1 - \frac{{\sqrt 3 }}{2}} \right) \approx 1,4\,\,\left( N \right)\)

Chọn D.