Phương pháp giải:

Sử dụng vòng tròn lượng giác và công thức \(\Delta t = \frac{{\Delta \varphi }}{\omega }\).

Áp dụng các công thức cực trị: \({v_{\max }} = \omega A;\,\,{a_{\max }} = {\omega ^2}A\) và công thức độc lập với thời gian: \({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2};\,\,a =  - {\omega ^2}x\).

Lời giải chi tiết:

Ta có: \(\left\{ \begin{array}{l}{v_{\max }} = \omega A = 300\,\,cm/s\\{a_{\max }} = {\omega ^2}A = 3000\pi \,\,cm/{s^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}A = \frac{{30}}{\pi }\,\,\left( {cm} \right)\\\omega  = 10\pi \,\,\left( {rad/s} \right)\end{array} \right.\)

Thời điểm ban đầu, vật có vận tốc 1,5 m/s = 150 cm/s, áp dụng công thức độc lập với thời gian, ta có:

\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow {x^2} + \frac{{{{150}^2}}}{{{{\left( {10\pi } \right)}^2}}} = {\left( {\frac{{30}}{\pi }} \right)^2} \Rightarrow x =  \pm \frac{{15\sqrt 3 }}{\pi }{\mkern 1mu} {\mkern 1mu} \left( {cm} \right) = \frac{{ \pm A\sqrt 3 }}{2}\)

Thế năng đang giảm \( \Rightarrow x = \frac{{ - A\sqrt 3 }}{2}\) và chuyển động theo chiều dương.

Thời điểm vật có gia tốc bằng \( - 15\pi \,\,m/{s^2}\), ta có: 

\(\begin{gathered}
a = - 15\pi \,\left( {m/{s^2}} \right) = - \frac{{30\pi }}{2} \Leftrightarrow a = - \frac{{{a_{\max }}}}{2} \hfill \\
\Leftrightarrow - {\omega ^2}x = - \frac{{{\omega ^2}A}}{2} \Rightarrow x = \frac{A}{2} \hfill \\
\end{gathered} \)

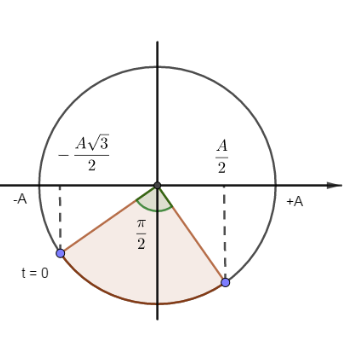
Từ VTLG, ta thấy vật chuyển động từ vị trí \(x = \frac{{ - A\sqrt 3 }}{2}\) đến vị trí \(x = \frac{A}{2}\), góc quét được là \(\frac{\pi }{2}\)

→ Thời điểm vật có gia tốc bằng \( - 15\pi \,\,m/{s^2}\): \(t = \frac{{\Delta \varphi }}{\omega } = \frac{{\frac{\pi }{2}}}{{10\pi }} = 0,05\,\,\left( s \right)\)

Chọn B.