Câu hỏi
Một con lắc lò xo đang dao động điều hòa với biên độ A, thời gian ngắn nhất để con lắc di chuyển từ vị trí có li độ \({x_1} = - A\) đến vị trí có li độ \({x_2} = \frac{A}{2}\) là 1s. Chu kì dao động của con lắc là
- A \(\frac{1}{3}\,\,s\).
- B 2 s.
- C 3 s.
- D 6 s.
Phương pháp giải:
Sử dụng vòng tròn lượng giác và công thức \(\Delta t = \frac{{\Delta \varphi }}{\omega }\).
Lời giải chi tiết:
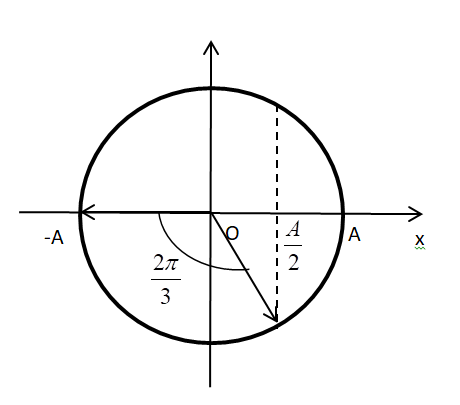
Từ VTLG, ta thấy vật đi từ vị trí có li độ \({x_1} = - A\) đến vị trí có li độ \({x_2} = \frac{A}{2}\), góc quét là \(\frac{{2\pi }}{3}\).
Áp dụng mối liên hệ giữa góc \(\Delta \varphi \) và thời điểm \(\Delta t\), ta có:
\(\Delta t = \frac{{\Delta \varphi }}{\omega } \Rightarrow \omega = \frac{{\Delta \varphi }}{{\Delta t}} = \frac{{\frac{{2\pi }}{3}}}{1} = \frac{{2\pi }}{3}\,\,\left( {rad/s} \right)\)
Chu kì dao động của con lắc: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{{2\pi }}{3}}} = 3\,\,\left( s \right)\)
Chọn C.
Câu hỏi trước
