Phương pháp giải:

Sử dụng vòng tròn lượng giác và công thức \(\Delta t = \frac{{\Delta \varphi }}{\omega }\); chiều dài quỹ đạo: L = 2.A

Lời giải chi tiết:

Biên độ dao động: \(A = \frac{L}{2} = \frac{{20}}{2} = 10\,\,cm\)

Vật đi được 10 cm thì tới vị trí có x = 5 và chưa đổi chiều → ban đầu vật ở li độ \({x_0} =  - 5\,cm\) và đang đi theo chiều dương.

Từ VTLG, ta biểu diễn được vị trí của vật tại các thời điểm:

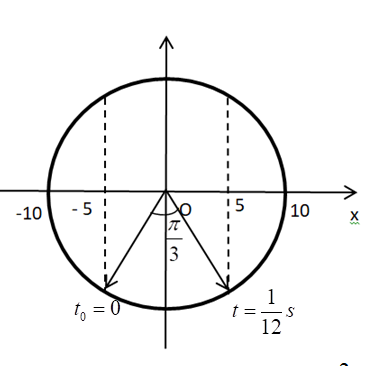
Vậy pha ban đầu của dao động: \(\varphi  =  - \frac{{2\pi }}{3}\,\,rad\)

Từ VTLG, ta thấy sau \(\frac{1}{{12}}s\) kể từ thời điểm ban đầu, vật đi từ li độ \({x_0} =  - 5\,cm\) tới \(x = 5\,cm\), góc quét được là \(\frac{\pi }{3}\).

Vậy áp dụng mối liên hệ giữa góc quét \(\Delta \varphi \) và khoảng thời gian ∆t, ta có:

\(\Delta \varphi  = \frac{\pi }{3} \Rightarrow \omega  = \frac{{\Delta \varphi }}{{\Delta t}} = \frac{{\frac{\pi }{3}}}{{\frac{1}{{12}}}} = 4{\mkern 1mu} \pi {\mkern 1mu} \,\,\left( {rad/s} \right)\)

Vậy phương trình dao động của vật: \(x = 10\cos \left( {4\pi t  - \frac{{2\pi }}{3}} \right)\,\,cm\)

Chọn A.