Phương pháp giải:

Sử dụng vòng tròn lượng giác và công thức \(\Delta t = \frac{{\Delta \varphi }}{\omega }\)

Lời giải chi tiết:

Thời gian vật đi qua vị trí cách vị trí cân bằng \(\frac{A}{2}\) lần thứ 2001 là: \({t_{2001}} = {t_{2000}} + {t_1}\)

Trong 1 chu kì, vật đi qua vị trí cách vị trí cân bằng \(\frac{A}{2}\) 4 lần \( \Rightarrow {t_{2000}} = 500T\)

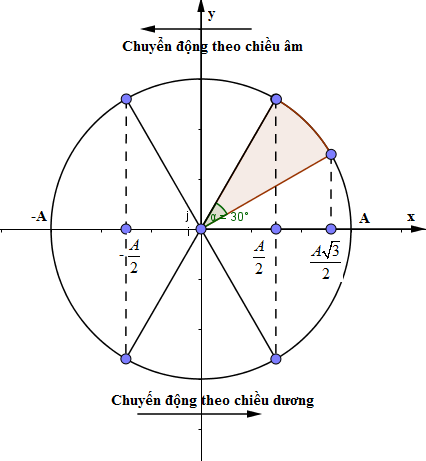
Từ VTLG, ta thấy thời điểm đầu tiên vật đi đến vị trí cách vị trí cân bằng \(\frac{A}{2}\) lần đầu tiên, vật quét được góc \(\frac{\pi }{6}\).

Vậy áp dụng mối liên hệ giữa góc quét \(\Delta \varphi \) và khoảng thời gian ∆t, ta có:

\(\Delta \varphi  = \frac{\pi }{6} \Rightarrow {t_1} = \frac{{\Delta \varphi }}{\omega } = \frac{{\frac{\pi }{6}}}{{\frac{{2\pi }}{T}}} = \frac{T}{{12}}\,\)

\( \Rightarrow {t_{2001}} = 500T + \frac{T}{{12}}\)

Chọn A.