Câu hỏi
Một vật dao động điều hòa từ A đến B với chu kỳ T, vị trí cân bằng O. Trung điểm OA, OB là M, N. Thời gian ngắn nhất để vật đi từ M đến N là \(\frac{1}{{30}}s\). Hãy xác định chu kỳ dao động của vật.
- A \(\frac{1}{4}s\)
- B \(\frac{1}{5}s\)
- C \(\frac{1}{{10}}s\)
- D \(\frac{1}{6}s\)
Phương pháp giải:
Sử dụng vòng tròn lượng giác và công thức \(\Delta t = \frac{{\Delta \varphi }}{\omega }\)
Lời giải chi tiết:
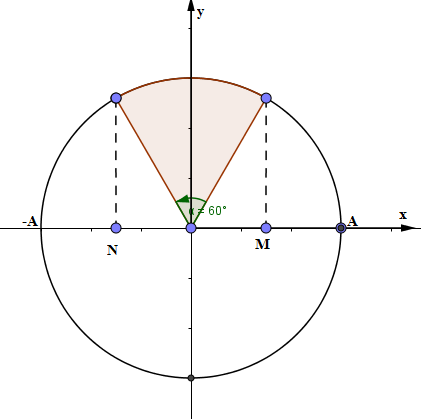
Từ VTLG, ta thấy thời gian ngắn nhất vật đi từ M đến N là \(\frac{1}{{30}}s\), vật quét được góc \(\frac{\pi }{3}\).
Vậy áp dụng mối liên hệ giữa góc quét \(\Delta \varphi \) và khoảng thời gian ∆t, ta có:
\(\omega = \frac{{\Delta \varphi }}{{\Delta t}} = \frac{{\frac{\pi }{3}}}{{\frac{1}{{30}}}} = 10\pi \,\,\left( {rad/s} \right)\).
Chu kì dao động: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{10\pi }} = \frac{1}{5}{\mkern 1mu} {\mkern 1mu} \left( s \right)\)
Chọn B.
Câu hỏi trước
