Câu hỏi
Cho tam giác ABC, gọi M là trung điểm của BC và I là trung điểm của AM.
1) Chứng minh rằng: \(2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \).
2) Với điểm O bất kỳ. Chứng minh: \(2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OI} \).
Lời giải chi tiết:
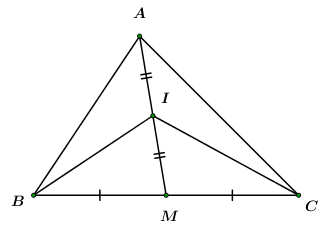
\(\begin{array}{l}1) \,\,\,2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = 2\overrightarrow {IA} + 2\overrightarrow {IM} \\ = 2\left( {\overrightarrow {IA} + \overrightarrow {IM} } \right) = 2.\overrightarrow 0 = \overrightarrow 0 \end{array}\)
\(\begin{array}{l}2)\,\,\,\,2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \\ \Leftrightarrow 2\left( {\overrightarrow {OA} - \overrightarrow {OI} } \right) + \left( {\overrightarrow {OB} - \overrightarrow {OI} } \right) + \left( {\overrightarrow {OC} - \overrightarrow {OI} } \right) = \overrightarrow 0 \\ \Leftrightarrow 2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} - 4\overrightarrow {OI} = \overrightarrow 0 \\ \Leftrightarrow 2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OI} \end{array}\)







