Câu hỏi
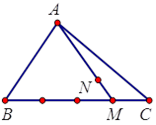
Cho tam giác \(ABC\) , trên cạnh BC lấy M sao cho \(BM = 3CM\), trên đoạn AM lấy N sao cho \(2AN = 5MN\). Phân tích các vectơ \(\overrightarrow {AM} ,{\rm{ }}\overrightarrow {BN} \) qua các véc tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \). Chọn khẳng định đúng nhất.
- A \(\overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \)
- B \(\overrightarrow {BN} = - \frac{{23}}{{28}}\overrightarrow {AB} + \frac{{15}}{{28}}\overrightarrow {AC} \)
- C Cả A, B đều đúng
- D Cả A,B đều sai
Phương pháp giải:
Sử dụng quy tắc 3 điểm, quy tắc trừ để biến đổi.
Lời giải chi tiết:
Theo giả thiết ta có: \(\overrightarrow {BM} = \frac{3}{4}\overrightarrow {BC} \) và \(\overrightarrow {AN} = \frac{5}{7}\overrightarrow {AM} \)
\(\begin{array}{l} \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + \frac{3}{4}\overrightarrow {BC} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \overrightarrow {AB} + \frac{3}{4}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} .\end{array}\)
\(\begin{array}{l}\overrightarrow {BN} = \overrightarrow {BA} + \overrightarrow {AN} = - \overrightarrow {AB} + \frac{5}{7}\overrightarrow {AM} \\\,\,\,\,\,\,\,\, = - \overrightarrow {AB} + \frac{5}{7}\left( {\frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} } \right)\\\,\,\,\,\,\,\,\, = - \frac{{23}}{{28}}\overrightarrow {AB} + \frac{{15}}{{28}}\overrightarrow {AC} .\end{array}\)
Chọn C.