Câu hỏi
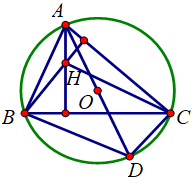
Cho tam giác \(ABC\) có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Chọn khẳng định đúng?
- A \(\overrightarrow {GH} + 2\overrightarrow {GO} = \overrightarrow {OA} \)
- B \(\overrightarrow {GH} + 2\overrightarrow {GO} = \overrightarrow 0 \)
- C \(\overrightarrow {GH} + 2\overrightarrow {GO} = \overrightarrow {AB} \)
- D \(\overrightarrow {GH} + 2\overrightarrow {GO} = \overrightarrow {AC} \)
Phương pháp giải:
Chứng minh \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} = 3\overrightarrow {OG} \)
Lời giải chi tiết:
Dễ thấy \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \) nếu tam giác \(ABC\) vuông
Nếu tam giác\(ABC\) không vuông gọi D là điểm đối xứng của A qua O khi đó
\(BH//DC\) (vì cùng vuông góc với AC)
\(BD//CH\) (vì cùng vuông góc với AB)
Suy ra \(BDCH\) là hình bình hành, do đó theo quy tắc hình bình hành thì \(\overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HD} \) (1)
Mặt khác vì O là trung điểm của AD nên \(\overrightarrow {HA} + \overrightarrow {HD} = 2\overrightarrow {HO} \) (2)
Từ (1) và (2) suy ra \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \)
\(\begin{array}{l} \Leftrightarrow \left( {\overrightarrow {HO} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {HO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {HO} + \overrightarrow {OC} } \right) = 2\overrightarrow {HO} \\ \Leftrightarrow 3\overrightarrow {HO} + \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 2\overrightarrow {HO} \\ \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} \end{array}\)
Vì G là trọng tâm tam giác \(ABC\) nên \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} \)
\( \Rightarrow \overrightarrow {OH} = 3\overrightarrow {OG} \Leftrightarrow \left( {\overrightarrow {OG} + \overrightarrow {GH} } \right) - 3\overrightarrow {OG} = \overrightarrow 0 \Leftrightarrow \overrightarrow {GH} + 2\overrightarrow {GO} = \overrightarrow 0 \)
Chọn B.