Lời giải chi tiết:

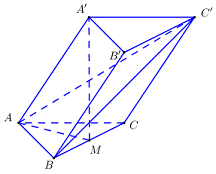
Góc giữa cạnh bên \(AA'\) và \(\left( {ABC} \right)\).

   A chung;

   \(A'M \bot \left( {ABC} \right)\);

\( \Rightarrow \) Góc giữa \(AA'\) và \(\left( {ABC} \right)\) là \(\widehat {A'AM} \Rightarrow \widehat {A'AM} = {60^0}\).

+ \(AM\) là đường cao trong tam giác đều \( \Rightarrow AM = \dfrac{{a\sqrt 3 }}{2}\).

+ \(\tan \widehat {A'AM} = \dfrac{{A'M}}{{AM}} \Leftrightarrow A'M = AM.\tan {60^0} = \dfrac{{a\sqrt 3 }}{2}.\sqrt 3  = \dfrac{{3a}}{2}\).

+ \({V_{ABC.A'B'C'}} = AM'.{S_{day}} = \dfrac{{3a}}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{a^3}\sqrt 3 }}{8}\).

\(\left. \begin{array}{l} + \,\,{V_{C'A'AB}} = \dfrac{1}{3}h{S_{A'AB}}\\\,\,\,\,{V_{C'A'B'BA}} = \dfrac{1}{3}h.{S_{A'B'BA}}\\\,\,\,\,{S_{A'AB}} = \dfrac{1}{2}{S_{A'B'BA}}\end{array} \right\} \Rightarrow {V_{C'A'AB}} = \dfrac{1}{2}{V_{C'A'B'BA}}\,\,\left( 1 \right)\)

\(\begin{array}{l} + \,\,{V_{C'A'B'BA}} = {V_{ABC.A'B'C'}} - {V_{C'ABC}} = {V_{ABC.A'B'C'}} - \dfrac{1}{3}{V_{ABC.A'B'C'}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{2}{3}{V_{ABC.A'B'C'}} = \dfrac{2}{3}.\dfrac{{3{a^3}\sqrt 3 }}{8} = \dfrac{{{a^3}\sqrt 3 }}{4}\,\,\,\left( 2 \right)\end{array}\)

Từ (1) và (2) \( \Rightarrow {V_{C'A'AB}} = \dfrac{1}{2}.\dfrac{{{a^3}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{8}\).

Chọn A