Lời giải chi tiết:

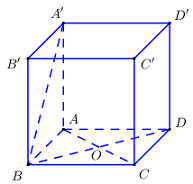
+ Xét tam giác \(ABC\) có \(\widehat B = {60^0};\,\,AB = BC\,\,\left( {gt} \right) \Rightarrow \Delta ABC\) đều.

\( \Rightarrow AC = AB = BC = a\). Mà \(O\) là trung điểm của \(AC \Rightarrow OA = \dfrac{a}{2}\).

+ \(ABCD\) là hình thoi \( \Rightarrow AC \bot BD \Rightarrow \Delta OAB\) vuông tại \(O\).

\( \Rightarrow O{A^2} + O{B^2} = A{B^2} \Leftrightarrow \dfrac{{{a^2}}}{4} + O{B^2} = {a^2} \Rightarrow OB = \dfrac{{a\sqrt 3 }}{2}\).

\( \Rightarrow BD = 2OB = 2\dfrac{{a\sqrt 3 }}{2} = a\sqrt 3 \).

+ Vì đường chéo của đáy lớn bằng đường chéo của lăng trụ \( \Rightarrow A'B = BD = a\sqrt 3 \).

+ Xét tam giác \(A'AB\) có \(A'A \bot AB\) (vì \(ABCD.A'B'C'D'\) là lăng trụ đứng).

\( \Rightarrow A'{A^2} + A{B^2} = A'{B^2} \Leftrightarrow A'{A^2} = A'{B^2} - A{B^2} = 3{a^2} - {a^2} = 2{a^2} \Rightarrow A'A = \sqrt 2 a\).

+ \({V_{ABCD.A'B'C'D'}} = AA'.{S_{ABCD}} = AA'.\dfrac{{AC.BD}}{{22}} = \sqrt 2 a\dfrac{{a.a\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 6 }}{2}\).

Chọn A