Câu hỏi
Cho lăng trụ đứng \(ABC.A'B'C'\)có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = a\sqrt 2 ,\,\,BC = 3a\). Góc giữa đường thẳng \(A'B\) và mặt đáy là \({60^0}\). Tính theo \(a\) thể tích khối lăng trụ \(ABC.A'B'C'\).
- A \(\dfrac{{{a^3}\sqrt 3 }}{2}\)
- B \(2{a^3}\sqrt 3 \)
- C \(3{a^3}\sqrt 3 \)
- D \(6{a^3}\sqrt 3 \)
Lời giải chi tiết:
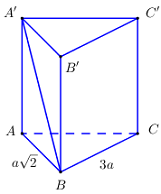
Xét tam giác \(A'AB\) vuông tại \(A\) có: \(AA' = \tan {60^0}.AB = \sqrt 3 .a\sqrt 2 = a\sqrt 6 \).
\({V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}} = a\sqrt 6 .\dfrac{1}{2}.AB.BC = a\sqrt 6 .\dfrac{1}{2}.a\sqrt 2 .3a = 3{a^3}\sqrt 3 \).
Chọn C
Câu hỏi trước
