Câu hỏi
Cho hình chóp tứ giác đều \(S.ABCD\). Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm của \(SB,{\rm{ }}SD\). Mặt phẳng \(\left( {AMN} \right)\) cắt \(SC\) tại \(E\). Gọi \({V_2}\) là thể tích của khối chóp \(S.AMEN\) và \({V_1}\) là thể tích khối chóp \(S.ABCD\). Khẳng định nào sau đây đúng?
- A \({V_2} = \dfrac{1}{3}{V_1}.\)
- B \({V_2} = \dfrac{1}{4}{V_1}.\)
- C \({V_2} = \dfrac{1}{8}{V_1}.\)
- D \({V_2} = \dfrac{1}{6}{V_1}.\)
Lời giải chi tiết:
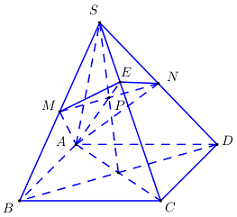
Gọi \(O = AC \cap BD,\,\,P = MN \cap SO,\,\,E' = AP \cap SC\).
\( \Rightarrow E' \in \left( {AMN} \right) \Rightarrow E' \equiv E\).
Áp dụng định lí Menelaus cho tam giác \(SPC\) có 3 điểm thẳng hàng là \(A,\,\,P,\,\,E\) ta có: \(\dfrac{{SE}}{{EC}}.\dfrac{{AC}}{{AO}}.\dfrac{{PO}}{{PS}} = 1\).
Mà \(MN\parallel BD \Rightarrow \dfrac{{PS}}{{PO}} = \dfrac{{SM}}{{MB}} = 1\).
\( \Rightarrow \dfrac{{SE}}{{EC}} = \dfrac{1}{2} \Rightarrow \dfrac{{SE}}{{SC}} = \dfrac{1}{3}\).
\(\begin{array}{l}\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABD}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SD}} = \dfrac{1}{4}\\\dfrac{{{V_{S.EMN}}}}{{{V_{S.CBD}}}} = \dfrac{{SE}}{{SC}}.\dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SD}} = \dfrac{1}{{12}}\\ \Rightarrow {V_2} = {V_{S.AMN}} + {V_{S.EMN}} = \dfrac{{{V_{S.ABD}}}}{4} + \dfrac{{{V_{S.CBD}}}}{{12}}\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{{V_{S.ABCD}}}}{8} + \dfrac{{{V_{S.ABCD}}}}{{24}} = \dfrac{{{V_1}}}{6}\end{array}\)
Chọn D







