Lời giải chi tiết:

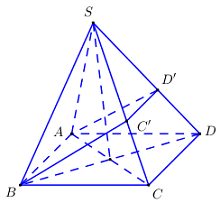
Qua \(C'\) kẻ \(C'D'\parallel CD\,\,\left( {D' \in SD} \right)\), ta có: \(C'D'\parallel CD\parallel AB \Rightarrow D' \in \left( {ABC'} \right)\).

Đặt \(\dfrac{{SD'}}{{SD}} = \dfrac{{SC'}}{{SC}} = k\,\,\left( {CD\parallel C'D'} \right)\,\,\left( {0 < k < 1} \right)\).

\(\begin{array}{l} \Rightarrow \dfrac{{{V_{S.AC'B}}}}{{{V_{S.ACB}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SC'}}{{SC}}.\dfrac{{SB}}{{SB}} = k\\\,\,\,\,\,\,\dfrac{{{V_{S.AC'D'}}}}{{{V_{S.ACD}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SC'}}{{SC}}.\dfrac{{SD'}}{{SD}} = {k^2}\\ \Rightarrow {V_{S.ABC'D'}} = {V_{S.AC'B}} + {V_{S.AC'D'}} = k{S_{S.ACB}} + {k^2}{V_{S.ACD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\left( {k + {k^2}} \right){V_{S.ABCD}}}}{2} = \dfrac{{{V_{S.ABCD}}}}{2}\\ \Rightarrow {k^2} + k - 1 = 0 \Leftrightarrow k = \dfrac{{\sqrt 5  - 1}}{2}\,\,\left( {Do\,\,k > 0} \right)\end{array}\).

Chọn C