Câu hỏi
Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh đều bằng \(a.\) Gọi \(M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q\) lần lượt thuộc các cạnh \(SA,{\rm{ }}SB,{\rm{ }}SC,{\rm{ }}SD\) sao cho \(\overrightarrow {SM} = \overrightarrow {MA} ;{\rm{ }}\overrightarrow {SN} = 2\overrightarrow {NB} ;{\rm{ }}\overrightarrow {SP} = 3\overrightarrow {PC} ;{\rm{ }}\overrightarrow {SQ} = \dfrac{1}{3}\overrightarrow {SD} .\) Tính thể tích khối \(SMNPQ.\)
- A \(\dfrac{{3\sqrt 2 {a^3}}}{{16}}.\)
- B \(\dfrac{{\sqrt 2 {a^3}}}{{48}}.\)
- C \(\dfrac{{\sqrt 2 {a^3}}}{{16}}.\)
- D \(\dfrac{{\sqrt 2 {a^3}}}{{32}}.\)
Lời giải chi tiết:
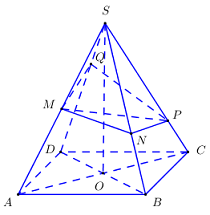
\(\begin{array}{l}\dfrac{{{V_{S.MQP}}}}{{{V_{S.ADC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SQ}}{{SD}}.\dfrac{{SP}}{{SC}} = \dfrac{1}{8}\\\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}} = \dfrac{1}{4}\\ \Rightarrow {V_{S.MNPQ}} = {V_{S.MQP}} + {V_{S.MNP}} = \dfrac{{{V_{S.ADC}}}}{8} + \dfrac{{{V_{S.ABC}}}}{4} = \dfrac{{3{V_{S.ABCD}}}}{{16}}\\OB = \dfrac{{DB}}{2} = \dfrac{{a\sqrt 2 }}{2} \Rightarrow SO = \sqrt {S{B^2} - O{B^2}} = \dfrac{{a\sqrt 2 }}{2}\\ \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 2 }}{2}.{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\\ \Rightarrow {V_{S.MNPQ}} = \dfrac{{3{V_{S.ABCD}}}}{{16}} = \dfrac{{\sqrt 2 {a^3}}}{{32}}\end{array}\)
Chọn D







