Câu hỏi
Cho hình chóp \(S.ABC\). Gọi \(M,{\rm{ }}N\) lần lượt thuộc các cạnh \(SB,{\rm{ }}SC\) sao cho \(SM = MB,{\rm{ }}\overrightarrow {SN} = - 2\overrightarrow {CN} .\) Mặt phẳng \(\left( {AMN} \right)\) chia khối chóp thành hai phần, gọi \({V_1} = {V_{S.AMN}}\) và \({V_2} = {V_{ABCNM}}\). Khẳng định nào sau đây đúng?
- A \({V_1} = {V_2}.\)
- B \({V_1} = \dfrac{1}{3}{V_2}.\)
- C \({V_1} = \dfrac{1}{2}{V_2}.\)
- D \({V_1} = \dfrac{2}{3}{V_2}.\)
Lời giải chi tiết:
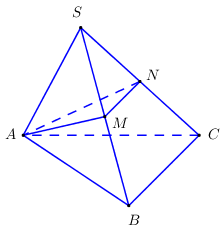
Ta có: Áp dụng định lí Simson:
\( \Rightarrow \dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SC}} = \dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{3}\).
\( \Rightarrow \dfrac{{{V_{AMNBC}}}}{{{V_{S.ABC}}}} = \dfrac{{{V_{S.ABC}} - {V_{S.AMN}}}}{{{V_{S.ABC}}}} = 1 - \dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = 1 - \dfrac{1}{3} = \dfrac{2}{3}\).
\( \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{{V_{S.AMN}}}}{{{V_{AMNBC}}}} = \dfrac{{\dfrac{1}{3}}}{{\dfrac{2}{3}}} = \dfrac{1}{2}\).
Chọn C
Câu hỏi trước
