Lời giải chi tiết:

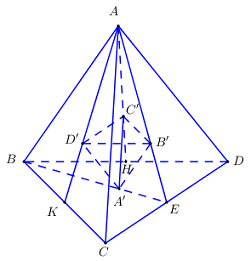
\(E\) là trung điểm của \(CD\)

\(K\) là trung điểm của \(BC\)

\(H\) là trung điểm của \(BD\)

Có \(\dfrac{{EB'}}{{EA}} = \dfrac{{EA'}}{{EB}} = \dfrac{1}{3} \Rightarrow A'B'\parallel AB\)\( \Rightarrow A'B' = \dfrac{1}{3}AB\) hay \(\dfrac{{A'B'}}{{AB}} = \dfrac{1}{3}\).

Có \(\dfrac{{KD'}}{{KA}} = \dfrac{{KA'}}{{KD}} = \dfrac{1}{3} \Rightarrow A'D'\parallel AD\)\( \Rightarrow A'D' = \dfrac{1}{3}AD\) hay \(\dfrac{{A'D'}}{{AD}} = \dfrac{1}{3}\).

Có \(\dfrac{{HC'}}{{HA}} = \dfrac{{HA'}}{{GC}} = \dfrac{1}{3} \Rightarrow A'C'\parallel AC \Rightarrow A'C' = \dfrac{1}{3}AC\) hay \(\dfrac{{A'C'}}{{AC}} = \dfrac{1}{3}\).

\(\dfrac{{{V_{A'B'C'D'}}}}{{{V_{ABCD}}}} = \dfrac{{A'B'}}{{AB}}.\dfrac{{A'C'}}{{AC}}.\dfrac{{A'D'}}{{AD}} = {\left( {\dfrac{1}{3}} \right)^3} = \dfrac{1}{{27}}\).

\( \Rightarrow {V_{A'B'C'D'}} = \dfrac{V}{{27}}\).

Chọn D