Câu hỏi
Cho hình chóp \(S.ABCD\) có \(SA\) vuông góc với đáy. Đáy là hình chữ nhật với \(AB = a,\)\(AC = a\sqrt 5 \), \(SA = a\). \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(SB,\,\,SC,\,\,SD\). Tính \({V_{SAMNP}}\) ?
- A \(V = \dfrac{{{a^3}}}{{12}}\)
- B \(V = \dfrac{{{\rm{2}}{a^3}}}{3}\)
- C \(V = \dfrac{{{a^3}}}{6}\)
- D \(V = \dfrac{{{a^3}}}{3}\)
Lời giải chi tiết:
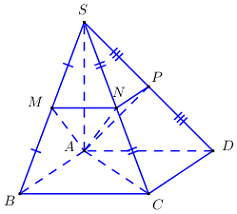
+ \(BC = \sqrt {A{C^2} - A{B^2}} = 2a\).
\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.a.a.2a = \dfrac{{2{a^3}}}{3}\).
+ \(\left\{ \begin{array}{l}\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SC}} = \dfrac{1}{4}\\{V_{S.ABC}} = \dfrac{1}{2}{V_{S.ABCD}}\end{array} \right. \Rightarrow {V_{S.AMN}} = \dfrac{1}{8}{V_{S.ABCD}}\)
Tương tự: \({V_{S.ANP}} = \dfrac{1}{8}{V_{S.ABCD}}\).
\(\begin{array}{l} \Rightarrow {V_{S.AMNP}} = {V_{S.AMN}} + {V_{S.ANP}} = \dfrac{1}{8}{V_{S.ABCD}} + \dfrac{1}{8}{V_{S.ABCD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{4}{V_{S.ABCD}} = \dfrac{1}{4}.\dfrac{{2{a^3}}}{3} = \dfrac{{{a^3}}}{6}\end{array}\).
Chọn C
Câu hỏi trước
