Câu hỏi
Cho hình chóp \(S.ABC\), \(SA\) vuông góc với mặt phẳng đáy, \(SA = 2a\), đáy \(ABC\) là tam giác đều cạnh \(a\). Kẻ \(AH \bot SB,\,\,AK \bot SC\). Thể tích khối chóp \(SAHK\) là:
- A \(V = \dfrac{{8{a^3}\sqrt 3 }}{{75}}\)
- B \(V = \dfrac{{8{a^3}}}{{15}}\)
- C \(V = \dfrac{{{a^3}\sqrt 8 }}{5}\)
- D \(V = \dfrac{{9{a^3}\sqrt 3 }}{{75}}\)
Lời giải chi tiết:
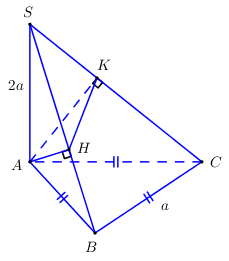
+ \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{\Delta ABC}} = \dfrac{1}{3}.2a.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{6}\).
+ \(S{A^2} = SH.SB \Rightarrow {\left( {\dfrac{{SA}}{{SB}}} \right)^2} = \dfrac{{SH}}{{SB}} = \dfrac{{4{a^2}}}{{5{a^2}}} = \dfrac{4}{5}\). Tương tự: \(\dfrac{{SK}}{{SC}} = \dfrac{4}{5}\).
+ \(\dfrac{{{V_{S.AHK}}}}{{{V_{S.ABC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SH}}{{SB}}.\dfrac{{SK}}{{SC}} = \dfrac{{16}}{{25}}\).
\( \Rightarrow {V_{S.AHK}} = \dfrac{{16}}{{25}}.\dfrac{{{a^3}\sqrt 3 }}{6} = \dfrac{{8{a^3}\sqrt 3 }}{{75}}\).
Chọn A
Câu hỏi trước
