Câu hỏi
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với đáy, \(SA = 2a\). Đáy là tam giác \(ABC\) cân tại \(A\), \(AB = a\) , góc \(\widehat {BAC} = {120^0}\). Gọi \(M,\,\,N\) là hình chiếu của \(A\) lên \(SB,\,\,SC\). Tính \({V_{SAMN}}\).
- A \(V = \dfrac{{{\rm{8}}{a^3}\sqrt 3 }}{{75}}\)
- B \(V = \dfrac{{16{a^3}\sqrt 3 }}{{25}}\)
- C \(V = \dfrac{{{\rm{8}}{a^3}}}{{15}}\)
- D \(V = \dfrac{{9{a^3}\sqrt 3 }}{{75}}\)
Lời giải chi tiết:
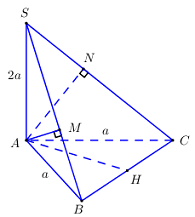
+ Xét tam giác \(ABC\) đều. Gọi \(H\) là trung điểm của \(BC\).
\( \Rightarrow AH\) là phân giác của \(\widehat {BAC}\) và \(AH\) là đường cao của tam giác \(ABC\).
\( \Rightarrow \widehat {BAH} = \widehat {HAC} = \dfrac{{\widehat {BAC}}}{2} = \dfrac{{{{120}^0}}}{2} = {60^0}\).
+ Xét tam giác \(ABH\,\,\left( {\widehat {AHB} = {{90}^0}} \right)\) có: \(\cos \widehat {BAM} = \dfrac{{AH}}{{AB}} \Leftrightarrow AH = \dfrac{1}{2}a\).
\(\sin \widehat {BAH} = \dfrac{{BH}}{{AB}} \Leftrightarrow \sin {60^0} = \dfrac{{BH}}{a} \Leftrightarrow BH = \dfrac{{\sqrt 3 }}{2}a\).
Mà \(H\) là trung điểm của \(BC \Rightarrow BC = 2BH = \sqrt 3 a\).
\( \Rightarrow {S_{\Delta ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.\dfrac{1}{2}a.\sqrt 3 a = \dfrac{{\sqrt 3 }}{4}{a^2}\).
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SA.{S_{\Delta ABC}} = \dfrac{1}{3}.2a.\dfrac{{\sqrt 3 }}{4}{a^2} = \dfrac{{\sqrt 3 }}{6}{a^3}\).
Xét \(\Delta SAB\) có \(\widehat {SAB} = {90^0},\,\,AM\) là đường cao) \( \Rightarrow \dfrac{1}{{A{M^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{B^2}}} = \dfrac{1}{{{{\left( {2a} \right)}^2}}} + \dfrac{1}{{{a^2}}} \Leftrightarrow AM = \dfrac{{2a}}{{\sqrt 5 }}\).
+ Xét \(\Delta SAM\,\,\left( {\widehat {SAM} = {{90}^0}} \right)\) : \(A{M^2} + S{M^2} = S{A^2}\,\,\left( {Pytago} \right) \Leftrightarrow {\left( {\dfrac{{2a}}{{\sqrt 5 }}} \right)^2} + S{M^2} = {\left( {2a} \right)^2} \Leftrightarrow SM = \dfrac{{4\sqrt 5 }}{5}a\).
+ Xét \(\Delta SAB\,\,\left( {\widehat {SAB} = {{90}^0}} \right)\) : \(S{A^2} + A{B^2} = S{B^2}\,\,\left( {Pytago} \right) \Leftrightarrow {\left( {2a} \right)^2} + {a^2} = S{B^2} \Leftrightarrow SB = \sqrt 5 a\).
+ Xét \(\Delta SAC\,\,\left( {\widehat {SAC} = {{90}^0}} \right)\) có : \(S{A^2} + A{C^2} = S{C^2}\,\,\left( {Pytago} \right) \Leftrightarrow {\left( {2a} \right)^2} + {a^2} = S{C^2} \Leftrightarrow SC = \sqrt 5 a\).
Áp dụng HTL trong tam giác vuông ta có: \(SN.SC = S{A^2} \Rightarrow SN = \dfrac{{{{\left( {2a} \right)}^2}}}{{\sqrt 5 a}} = \dfrac{4}{{\sqrt 5 }}a\).
\(\begin{array}{l}\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SC}} = 1.\dfrac{{\dfrac{{4\sqrt 5 }}{5}a}}{{\sqrt 5 a}}.\dfrac{{\dfrac{4}{{\sqrt 5 }}a}}{{\sqrt 5 a}} = \dfrac{{16}}{{25}}\\ \Rightarrow {V_{S.AMN}} = \dfrac{{16}}{{25}}.\dfrac{{\sqrt 3 }}{6}{a^3} = \dfrac{{8\sqrt 3 {a^3}}}{{75}}\end{array}\)
Chọn A







