Câu hỏi
Cho hình chóp \(S.ABC\)có \(SA\) vuông góc với đáy. Tam giác \(ABC\) vuông cân tại \(B\), \(AB = a\sqrt 2 \). Gọi \(G\) là trọng tâm của tam giác \(SBC\). Mặt phẳng qua \(AG\) và song song với \(BC\) cắt \(SB,\,\,SC\) lần lượt tại \(B',\,\,C'\). Tính \({V_{B'C'ABC}}\) biết \(SA = a\)?
- A \(V = \dfrac{{5{a^3}}}{9}\)
- B \(V = \dfrac{{5{a^3}}}{{27}}\)
- C \(V = \dfrac{{4{a^3}}}{9}\)
- D \(V = \dfrac{{4{a^3}}}{{27}}\)
Lời giải chi tiết:
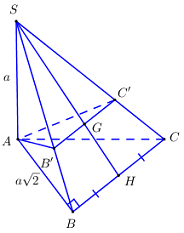
+ Qua \(G\) kẻ \(d//BC,\,\,d \cap SB = B',\,\,d \cap SC = C'\).
\( \Rightarrow \left( {AB'C'} \right)\parallel BC\).
+ \(G\) là trọng tâm tam giác \(SBC \Rightarrow \dfrac{{SG}}{{SH}} = \dfrac{2}{3}\).
\(B'C'\parallel BC \Rightarrow \dfrac{{SB'}}{{SB}} = \dfrac{{SC'}}{{SC}} = \dfrac{{SG}}{{SH}} = \dfrac{2}{3}\).
+ \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.a.\dfrac{1}{2}a\sqrt 2 .a\sqrt 2 = \dfrac{{{a^3}}}{3}\).
+ \(\left. \begin{array}{l}\dfrac{{{V_{S.AB'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}} = \dfrac{4}{9}\\{V_{S.AB'C'}} + {V_{B'C'ABC}} = {V_{S.ABC}}\end{array} \right\} \Rightarrow {V_{B'C'ABC}} = \dfrac{5}{9}{V_{S.ABC}} = \dfrac{{5{a^3}}}{{27}}\).
Chọn B







