Câu hỏi
Cho tứ diện \(ABCD\) có thể tích bằng \(V\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AB,\,\,AC\). Tính thể tích của khối đa diện \(MNBCD\).
- A \(\dfrac{{3V}}{4}\)
- B \(\dfrac{V}{4}\)
- C \(\dfrac{V}{2}\)
- D \(\dfrac{{2V}}{3}\)
Lời giải chi tiết:
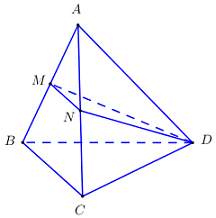
+ \(\dfrac{{{V_{AMND}}}}{{{V_{ABCD}}}} = \dfrac{{AM}}{{AB}}.\dfrac{{AN}}{{AC}}.\dfrac{{AD}}{{AD}} = \dfrac{1}{4}\).
\( \Rightarrow {V_{AMND}} = \dfrac{1}{4}{V_{ABCD}}\).
\({V_{AMND}} + {V_{MNBCD}} = {V_{ABCD}} \Rightarrow {V_{MNBCD}} = \dfrac{3}{4}{V_{ABCD}}\).
Vậy \({V_{MNBCD}} = \dfrac{3}{4}V\).
Chọn A
Câu hỏi trước
