Câu hỏi
Cho hình chóp \(S.ABC\) với tam giác \(ABC\) vuông cân tại \(B\), \(AC = 2a,\,\,SA \bot \left( {ABC} \right)\) và \(SA = a\). Trên cạnh \(SB\) lấy điểm \(I\) sao cho \(SI = \dfrac{1}{3}SB\). Tính thể tích tứ diện \(S.AIC\).
- A \({V_{SAIC}} = \dfrac{{{a^3}}}{9}\)
- B \({V_{SAIC}} = \dfrac{{{a^3}}}{3}\)
- C \({V_{SAIC}} = \dfrac{{2{a^3}}}{3}\)
- D \({V_{SAIC}} = \dfrac{{{a^3}}}{6}\)
Lời giải chi tiết:
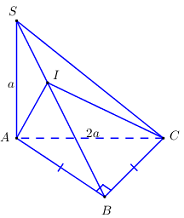
+ Tam giác \(ABC\) vuông cân tại \(B,\,\,AC = 2a\).
\( \Rightarrow AB = \dfrac{{AC}}{{\sqrt 2 }} = BC = \dfrac{{2a}}{{\sqrt 2 }} = a\sqrt 2 \).
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.BC = {a^2}\).
+ \(\dfrac{{{V_{SAIC}}}}{{{V_{SABC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SI}}{{SB}}.\dfrac{{SC}}{{SC}} = \dfrac{1}{3} \Rightarrow {V_{SAIC}} = \dfrac{1}{3}{V_{SABC}} = \dfrac{{{a^3}}}{9}\).
Chọn A
Câu hỏi trước
