Câu hỏi
Cho khối chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\); biết\(AB = A{\rm{D}} = 2a,\)\(C{\rm{D}} = a.\) Gọi \(I\) là trung điểm của \(AD\), biết hai mặt phẳng \(\left( {SBI} \right)\) và \(\left( {SCI} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Khoảng cách từ \(I\) đến mặt phẳng \(\left( {SBC} \right)\) bằng \(a\). Tính thể tích \(V\) khối chóp \(S.ABCD\).
- A \(V = \dfrac{{3\sqrt {15} {a^3}}}{8}\)
- B \(V = \dfrac{{9{a^3}}}{2}\)
- C \(V = \dfrac{{3\sqrt {15} {a^3}}}{5}\)
- D \(V = \dfrac{{3{a^3}}}{2}\)
Lời giải chi tiết:
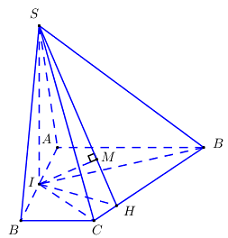
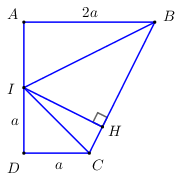
Chọn \(a = 2\), vẽ đúng kích thước đáy.
+ \(\left\{ \begin{array}{l}IH \bot BC\\IM \bot SH\end{array} \right. \Rightarrow IM = d\left( {I;\left( {SBC} \right)} \right)\).
+ Đo được \(IH \approx 2,8\).
\( \Rightarrow \dfrac{1}{{S{I^2}}} = \dfrac{1}{{I{M^2}}} - \dfrac{1}{{I{H^2}}} = \dfrac{1}{{{2^2}}} - \dfrac{1}{{2,{8^2}}} = 2,86\).
\( \Rightarrow {S_{ABCD}} = \dfrac{1}{2}\left( {AB + C{\rm{D}}} \right).AD = \dfrac{1}{2}\left( {4 + 2} \right).4 = 12\).
\(V = \dfrac{1}{3}SI.{S_{ABCD}} = \dfrac{1}{3}.2,86.12 = 11,5 \approx 12\).
Chọn D







