Câu hỏi
Cho tứ diện \(ABCD\). Các điểm \(B',\,\,C',\,\,D'\) lần lượt thuộc các tia \(AB,\,\,AC,\,\,AD\). Công thức nào dưới đây là đúng:
- A \(\dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}} = d\frac{{A{\rm{D}}'}}{{A{\rm{D}}}}\)
- B \(\dfrac{{AB'}}{{AB}} + \dfrac{{AC'}}{{AC}} + \dfrac{{A{\rm{D}}'}}{{A{\rm{D}}}} = 3\)
- C \(\dfrac{{{V_{ABC'D'}}}}{{{V_{ABC{\rm{D}}}}}} = \dfrac{{AB'.AC'.A{\rm{D}}'}}{{AB.AC.A{\rm{D}}}}\)
- D \(\dfrac{{{V_{ABC'D'}}}}{{{V_{ABC{\rm{D}}}}}} = \dfrac{{AB.AC.A{\rm{D}}}}{{AB'.AC'.A{\rm{D}}'}}\)
Lời giải chi tiết:
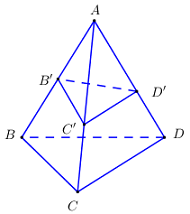
Theo định lí Simson có: \(\dfrac{{{V_{A.B'C'D'}}}}{{{V_{ABCD}}}} = \dfrac{{AB'}}{{AB}}.\dfrac{{AC'}}{{AC}}.\dfrac{{AD'}}{{AD}}\).
Chọn C
Câu hỏi trước
