Câu hỏi
Cho hình chóp \(S.ABCD\) đáy \(ABCD\)là hình vuông cạnh \(a\), \(\Delta SAB\) vuông cân tại \(S\),\(\Delta SCD\) đều . Tính thể tích khối chóp \(S.ABCD.\)
- A \(\dfrac{{{a^3}\sqrt 3 }}{{12}}\)
- B \(\dfrac{{{a^3}\sqrt 3 }}{4}\)
- C \(\dfrac{{{a^3}\sqrt 3 }}{6}\)
- D \(\dfrac{{{a^3}}}{6}\)
Lời giải chi tiết:
\(\dfrac{{{V_{S.ABC}}}}{{{V_{S.ACD}}}} = \dfrac{{\dfrac{1}{3}h.{S_{\Delta ABC}}}}{{\dfrac{1}{3}h.{S_{\Delta ACD}}}}\). Do \({S_{\Delta ABC}} = {S_{\Delta ACD}} \Rightarrow {V_{S.ABC}} = {V_{S.ACD}}\).
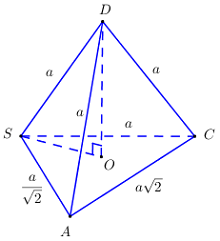
Do \(DS = DA = DC = a \Rightarrow \) Chiều cao \(DO\) với \(O\) là tâm \(\Delta SAC\).
\(\begin{array}{l}{S_{\Delta SAC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \\\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {\left( {\dfrac{{2 + 3\sqrt 2 }}{4}} \right)\left( {\dfrac{{2 + 3\sqrt 2 }}{4} - 1} \right)\left( {\dfrac{{2 + 3\sqrt 2 }}{4} - \sqrt 2 } \right)\left( {\dfrac{{2 + 3\sqrt 2 }}{4} - \dfrac{1}{{\sqrt 2 }}} \right)} = \dfrac{{\sqrt 7 }}{8}\end{array}\)
\(SO = r = \dfrac{{SA.SC.AC}}{{4{S_{\Delta SAC}}}} = \dfrac{{1.\sqrt 2 .\dfrac{1}{{\sqrt 2 }}}}{{4.\dfrac{{\sqrt 7 }}{8}}} = \dfrac{{2\sqrt 7 }}{7}\).
\( \Rightarrow DO = \sqrt {D{S^2} - S{O^2}} = \sqrt {{1^2} - {{\left( {\dfrac{{2\sqrt 7 }}{7}} \right)}^2}} = \dfrac{{\sqrt {21} }}{7}\).
\( \Rightarrow V = \dfrac{1}{3}.\dfrac{{\sqrt {21} }}{7}.\dfrac{{\sqrt 7 }}{8} = \dfrac{{\sqrt 3 }}{{24}}\).
\( \Rightarrow {V_{S.ABCD}} = 2{V_{S.ACD}} = 2.\dfrac{{\sqrt 3 }}{{24}} = \dfrac{{\sqrt 3 }}{{12}}\).
Chọn A







