Câu hỏi
Cho hình chóp \(S.ABC\), có\(\left( {SAC} \right) \bot \left( {ABC} \right)\), tam giác \(ABC\) đều cạnh \(a\). Biết rằng hai mặt phẳng \(\left( {SAB} \right)\,,\,\,\left( {SBC} \right)\)cùng tạo với đáy một góc \({60^0}\). Tính thể tích khối chóp \(S.ABC\).
- A \(\dfrac{{{a^3}\sqrt 3 }}{{16}}\)
- B \(\dfrac{{2{a^3}\sqrt 3 }}{8}\)\(\)
- C \(\dfrac{{{a^3}\sqrt 3 }}{8}\)
- D \(\dfrac{{2{a^3}\sqrt 3 }}{{16}}\)
Lời giải chi tiết:
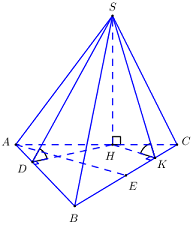
Kẻ \(SH \bot AC \Rightarrow SH \bot \left( {ABC} \right)\). Kẻ \(\left\{ \begin{array}{l}DH \bot AB\\HK \bot BC\end{array} \right. \Rightarrow \) Góc giữa \(\left( {SAB} \right)\) và \(\left( {ABC} \right)\) là \(\widehat {SDH} = {60^0}\) ; góc giữa \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) là \(\widehat {SKH} = {60^0}\).
\( \Rightarrow DH = KH\).
\( \Rightarrow \Delta SHD = \Delta SHK \Rightarrow SD = SK\).
Có \(\Delta ABC\) đều mà \(DH = HK \Rightarrow H\) là trung điểm của \(AC\).
Lấy \(E\) là trung điểm của \(BC,\,\,\Delta ABC\) đều \( \Rightarrow AE \bot BC\), mà \(HK \bot BC\).
\( \Rightarrow HK\) là đường trung bình của tam giác \(AEC\).
\( \Rightarrow HK = \dfrac{1}{2}AE = \dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{4}\).
Xét tam giác \(SHK\) vuông tại \(H\) có: \(SH = HK.tan\widehat {SKH} = \dfrac{{a\sqrt 3 }}{4}.\tan {60^0} = \dfrac{{3a}}{4}\).
\({V_{S.ABC}} = \dfrac{1}{3}SH.{S_{\Delta ABC}} = \dfrac{1}{3}.\dfrac{{3a}}{4}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{16}}\).
Chọn A







