Câu hỏi
Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(B\), \(AB = 3a,\,\,AC = 4a\), \(\left( {SBC} \right) \bot \left( {ABC} \right)\), \(SB = 2a\sqrt 3 ,\,\,\widehat {SBC} = {30^0}\). Thể tích của \(S.ABC\) là:
- A \(2{a^3}\sqrt 3 \)
- B \(\dfrac{2}{3}{a^3}\sqrt 3 \)
- C \(3{a^3}\sqrt 3 \)
- D \(\dfrac{1}{3}{a^3}\sqrt 3 \)
Lời giải chi tiết:
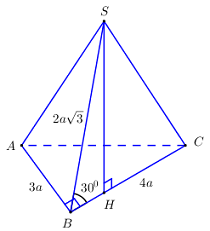
Kẻ \(SH \bot BC\), mà \(SH \subset \left( {SBC} \right);\,\,\left( {SBC} \right) \bot \left( {ABC} \right) \Rightarrow SH \bot \left( {ABC} \right)\).
Xét tam giác \(SHB\) vuông tại \(H\) có:
\(SH = SB.\sin \widehat {SBH} = 2a\sqrt 3 .\sin {30^0} = a\sqrt 3 \).
\({V_{S.ABC}} = \dfrac{1}{3}SH.{S_{\Delta ABC}} = \dfrac{1}{3}.SH.\dfrac{1}{2}.AB.BC = \dfrac{1}{3}a\sqrt 3 .\dfrac{1}{2}.3a.4a = 2\sqrt 3 {a^3}\).
Chọn A
Câu hỏi trước
