Câu hỏi
Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là \(a\). Thể tích \(V\) của khối chóp đó là:
- A \(V = \dfrac{{2\sqrt 2 }}{3}{a^3}\)
- B \(V = \dfrac{{4\sqrt 6 }}{{27}}{a^3}\)
- C \(V = \dfrac{{\sqrt 2 }}{6}{a^3}\)
- D \(V = \dfrac{{\sqrt 2 }}{9}{a^3}\)
Lời giải chi tiết:
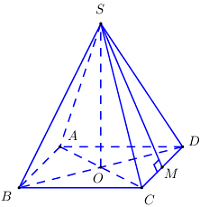
Gọi độ dài các cạnh của hình chóp là \(x\).
\( \Rightarrow SM = a = \dfrac{{x\sqrt 3 }}{2} \Rightarrow x = \dfrac{{2a}}{{\sqrt 3 }} = \dfrac{{2a\sqrt 3 }}{3}\).
\({S_{ABCD}} = {\left( {\dfrac{{2a\sqrt 3 }}{3}} \right)^2} = \dfrac{{4{a^2}}}{3}\).
\(SO = \sqrt {S{M^2} - O{M^2}} = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}} = \dfrac{{a\sqrt 6 }}{3}\)
\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{3}.\dfrac{{4{a^2}}}{3} = \dfrac{{4{a^3}\sqrt 6 }}{{27}}\).
Chọn B
Câu hỏi trước
