Lời giải chi tiết:

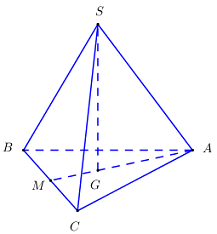
Xét hình chóp đều \(S.ABC\).

Gọi \(G\) là trọng tâm tam giác \(ABC \Rightarrow SG \bot \left( {ABC} \right)\).

Gọi \(M\) là trung điểm của \(BC\).

+ Xét \(\Delta ABC:\,\,AM = \dfrac{{a\sqrt 3 }}{2} \Rightarrow AG = \dfrac{2}{3}AM = \dfrac{{a\sqrt 3 }}{3}\).

+ \({S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\).

+ Xét \({\Delta _v}SAG\): \(S{G^2} = S{A^2} - A{G^2} = {\left( {2a} \right)^2} - {\left( {\dfrac{{a\sqrt 3 }}{3}} \right)^2} = \dfrac{{11{a^2}}}{3} \Rightarrow SG = a\sqrt {\dfrac{{11}}{3}} \).

\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SG.{S_{ABC}} = \dfrac{1}{3}.a\sqrt {\dfrac{{11}}{3}} .\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt {11} }}{{12}}\).

Chọn B