Câu hỏi
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy \(2a\) góc giữa mặt bên và mặt đáy bằng \({60^0}\). Tính thể tích hình chóp \(S.ABCD\).
- A \(\dfrac{{4{a^3}\sqrt 3 }}{3}\)
- B \(\dfrac{{{a^3}\sqrt 3 }}{3}\)
- C \(4{a^3}\sqrt 3 \)
- D \(\dfrac{{2{a^3}\sqrt 3 }}{3}\)
Lời giải chi tiết:
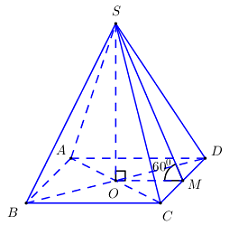
+ Gọi \(M\) là trung điểm của \(CD\).
\( \Rightarrow OM\parallel AD\) và \(OM = \dfrac{{AD}}{2} = \dfrac{{BC}}{2} = \dfrac{{2a}}{2} = a\).
+ Xét tam giác \(SOM\) vuông tại \(O\) có \(\tan \widehat {SMO} = \dfrac{{SO}}{{OM}} \Rightarrow SO = a\sqrt 3 \).
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.a\sqrt 3 .{\left( {2a} \right)^2} = \dfrac{{4{a^3}\sqrt 3 }}{3}\).
Chọn A
Câu hỏi trước
